「説明01」の版間の差分
ナビゲーションに移動
検索に移動
| (同じ利用者による、間の6版が非表示) | |||
| 1行目: | 1行目: | ||
<span id="説明01" style="font-size: 150% | <span id="説明01" style="font-size: 150%;">01:フィッティング方法</span> | ||
: 屈折率の分散をパラメータを使って表したい。ローレンツ関数<math>\frac{A}{\nu_l-\nu-i\gamma}</math>の重ね合わせによって<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>のように表せると考えている。理由は<u>[[ | : 屈折率の分散をパラメータを使って表したい。ローレンツ関数<math>\frac{A}{\nu_l-\nu-i\gamma}</math>の重ね合わせによって<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>のように表せると考えている。理由は<u>[[詳細01|詳細01]]</u>参照。 | ||
: 光の強度反射率について最小二乗法を行ってパラメータを決める。つまり、<math>[\left | r \right \vert_{calc}^2 - \left | r \right \vert_{exp}^2]^2</math>という式について最小二乗法を行っている。 | : 光の強度反射率について最小二乗法を行ってパラメータを決める。つまり、<math>[\left | r \right \vert_{calc}^2 - \left | r \right \vert_{exp}^2]^2</math>という式について最小二乗法を行っている。 | ||
: ここで<math>r</math>は両方とも電場の反射率である。光の強度反射率が電場の反射率の2乗になる理由は<ref name = "ref1" />参照 | : ここで<math>r</math>は両方とも電場の反射率である。光の強度反射率が電場の反射率の2乗になる理由は<ref name = "ref1" />参照 | ||
: <math>\left | r \right \vert_{exp}</math>については入力ファイルの値(単位が%)を100で割って用いる。 | : <math>\left | r \right \vert_{exp}</math>については入力ファイルの値(単位が%)を100で割って用いる。 | ||
: <math>\left | r \right \vert_{calc}^2</math>は<math>\frac{\left | r^s \right \vert_{calc}^2 + \left | r^p \right \vert_{calc}^2}{2}</math> | : <math>\left | r \right \vert_{calc}^2</math>は<math>\frac{\left | r^s \right \vert_{calc}^2 + \left | r^p \right \vert_{calc}^2}{2}</math> | ||
: のようにp波とs波の平均値で与えられる。詳細は<u>[[ | : のようにp波とs波の平均値で与えられる。詳細は<u>[[詳細02|詳細02]]</u> | ||
: また、各<math>r</math>はフレネルの公式 | : また、各<math>r</math>はフレネルの公式 | ||
: <math>r_s=\frac{n_1\cos{\theta}_i -n_2\cos{\theta}_t}{n_1\cos{\theta}_i +n_2\cos{\theta}_t}</math>, <math>r_p=\frac{n_2\cos{\theta}_i -n_1\cos{\theta}_t}{n_2\cos{\theta}_i +n_1\cos{\theta}_t}</math> | : <math>r_s=\frac{n_1\cos{\theta}_i -n_2\cos{\theta}_t}{n_1\cos{\theta}_i +n_2\cos{\theta}_t}</math>, <math>r_p=\frac{n_2\cos{\theta}_i -n_1\cos{\theta}_t}{n_2\cos{\theta}_i +n_1\cos{\theta}_t}</math> | ||
| 19行目: | 19行目: | ||
: <math>\gamma</math>は15とする。これは参考文献[2]<ref name = "ref2" />から、<math>\gamma</math>は15付近であるという傾向がわかっているからだ。 | : <math>\gamma</math>は15とする。これは参考文献[2]<ref name = "ref2" />から、<math>\gamma</math>は15付近であるという傾向がわかっているからだ。 | ||
: <math>A</math>は7.5とする。これは参考文献[2]<ref name = "ref2" />から、<math>A</math>と<math>\gamma</math>の間に<math>\frac{A}{\gamma} = {\kappa}_{max}</math>という関係があり、さらに<math>{\kappa}_{max}</math>が0.5付近の値を多くとるということがわかっているからだ。 | : <math>A</math>は7.5とする。これは参考文献[2]<ref name = "ref2" />から、<math>A</math>と<math>\gamma</math>の間に<math>\frac{A}{\gamma} = {\kappa}_{max}</math>という関係があり、さらに<math>{\kappa}_{max}</math>が0.5付近の値を多くとるということがわかっているからだ。 | ||
: 最後に<math>\nu_l</math>についてこれは入力④で与えられた解析範囲において入力⑤で読み込みを指定した列の反射率が最小になるところとしている。これはローレンツ関数<math>\frac{A}{\nu_l-\nu-i\gamma}</math>を実部と虚部に分けたとき、<math>\frac{A\gamma}{{\nu_l-\nu}^2 + {\gamma}^2} + i\frac{{\nu_l-\nu}^2}{{\nu_l-\nu}^2 + {\gamma}^2}</math>となり、虚部が吸収を表すことが関係している。虚部において最大になるところこそが<math>\nu_l</math> | : 最後に<math>\nu_l</math>についてこれは入力④で与えられた解析範囲において入力⑤で読み込みを指定した列の反射率が最小になるところとしている。これはローレンツ関数<math>\frac{A}{\nu_l-\nu-i\gamma}</math>を実部と虚部に分けたとき、<math>\frac{A\gamma}{{\nu_l-\nu}^2 + {\gamma}^2} + i\frac{{\nu_l-\nu}^2}{{\nu_l-\nu}^2 + {\gamma}^2}</math>となり、虚部が吸収を表すことが関係している。虚部において最大になるところこそが<math>\nu_l</math>であり、この時吸収は最大である。これは反射が最小に対応する。ゆえにこのように与えている。屈折率の虚部が吸収を表すことは[[詳細03|詳細03]]で説明している。 | ||
1つずつ与える。 | 1つずつ与える。 | ||
: 最小二乗法を行う際、パラメータの範囲はそれぞれ<math>A</math>は-200から200。<math>\nu_l</math>入力④で与えられた範囲。<math>\gamma</math>は0から500で行っている。 | : 最小二乗法を行う際、パラメータの範囲はそれぞれ<math>A</math>は-200から200。<math>\nu_l</math>入力④で与えられた範囲。<math>\gamma</math>は0から500で行っている。 | ||
| 26行目: | 26行目: | ||
: これが入力の⑩で与えられた値より小さければ結果を返す。 | : これが入力の⑩で与えられた値より小さければ結果を返す。 | ||
: 大きければ、ローレンツ関数を1つ増やす。この時、1つ目の初期値は今回の最小二乗法で求まった値を用いる。 | : 大きければ、ローレンツ関数を1つ増やす。この時、1つ目の初期値は今回の最小二乗法で求まった値を用いる。 | ||
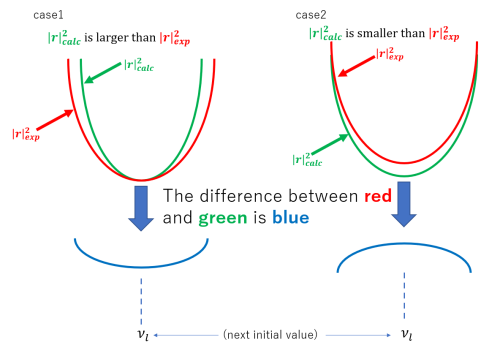
: 2つ目の初期値の作り方を説明する。これは、1つ目のローレンツ関数を用いて計算される <math>\left | r \right \vert_{calc}^2</math>を<math>\left | r \right \vert_{exp}^2</math> | : 2つ目の初期値の作り方を説明する。これは、1つ目のローレンツ関数を用いて計算される <math>\left | r \right \vert_{calc}^2</math>を<math>\left | r \right \vert_{exp}^2</math>から引いた値計算する。この差の関数のうち絶対値が最も大きい値に対応する波数を2つ目の<math>\nu_l</math>の初期値として与える。絶対値が最も大きな点が極大値の場合と極小値の場合の2パターンがある。模式的に示すと以下のようになる。 | ||
[[File:theory.png|500px]] | |||
[[File: | |||
: <math>A</math>の大きさは1つ目で求まったAの半分としている。これは屈折率の分散の概形が一つ目で与えられていると考え、足りない部分を補うという考えから、一つ目のAより小さいと考えたためである。今回はAの符号も検討する必要がある。これは、差の値が入力ファイルのように反射率が下に凸とは限らないからだ。よってνに対応する値が最小値なら正、最大値なら負というように与えている。最小値の場合、正として与えるのは1つ目の時と同じで反射率が最小の時吸収が最大になると考えるからである。逆の場合は、物理的な意味は考えづらいが数学的に符号を反対にすることが妥当だと考えたからである。 | : <math>A</math>の大きさは1つ目で求まったAの半分としている。これは屈折率の分散の概形が一つ目で与えられていると考え、足りない部分を補うという考えから、一つ目のAより小さいと考えたためである。今回はAの符号も検討する必要がある。これは、差の値が入力ファイルのように反射率が下に凸とは限らないからだ。よってνに対応する値が最小値なら正、最大値なら負というように与えている。最小値の場合、正として与えるのは1つ目の時と同じで反射率が最小の時吸収が最大になると考えるからである。逆の場合は、物理的な意味は考えづらいが数学的に符号を反対にすることが妥当だと考えたからである。 | ||
: 2回目以降も同じように残差が入力値より小さいかを判定して、小さければ結果を返し、大きければ1つ増やして、初期値を与えて、最小二乗法行う。これを結果が出るまで繰り返す。2回目以降の残差が大きかった場合の初期値の与え方は1回目と同じである。求まったパ:ラメータから計算される <math>\left | r \right \vert_{calc}^2</math>を<math>\left | r \right \vert_{exp}^2</math>から引いた値計算する。このうち絶対値が最も大きい値に対応する波数を2つ目の<math>\nu_l</math>の初期値として与える。<math>A</math>の大きさは1つ目で求まった<math>A</math>の半分としている。これは屈折率の分散の概形が一つ目で与えられていると考え、足りない部分を補うという考えから、一つ目のAより小さいと考えたためである。<math>A</math>の符号は<math>\nu_l</math>に対応する値が最小値なら正、最大値なら負というように与えている。 | : 2回目以降も同じように残差が入力値より小さいかを判定して、小さければ結果を返し、大きければ1つ増やして、初期値を与えて、最小二乗法行う。これを結果が出るまで繰り返す。2回目以降の残差が大きかった場合の初期値の与え方は1回目と同じである。求まったパ:ラメータから計算される <math>\left | r \right \vert_{calc}^2</math>を<math>\left | r \right \vert_{exp}^2</math>から引いた値計算する。このうち絶対値が最も大きい値に対応する波数を2つ目の<math>\nu_l</math>の初期値として与える。<math>A</math>の大きさは1つ目で求まった<math>A</math>の半分としている。これは屈折率の分散の概形が一つ目で与えられていると考え、足りない部分を補うという考えから、一つ目のAより小さいと考えたためである。<math>A</math>の符号は<math>\nu_l</math>に対応する値が最小値なら正、最大値なら負というように与えている。 | ||
| 40行目: | 37行目: | ||
<ref name = "ref1">遠藤雅守:電磁場の物理学ーその発生・伝搬・吸収・増幅・共振を電磁気学で理解するー</ref> | <ref name = "ref1">遠藤雅守:電磁場の物理学ーその発生・伝搬・吸収・増幅・共振を電磁気学で理解するー</ref> | ||
<ref name = "ref2">論文</ref> | <ref name = "ref2">論文</ref> | ||
<references | </references> | ||
2022年1月4日 (火) 01:33時点における最新版
01:フィッティング方法
- 屈折率の分散をパラメータを使って表したい。ローレンツ関数の重ね合わせによってのように表せると考えている。理由は詳細01参照。
- 光の強度反射率について最小二乗法を行ってパラメータを決める。つまり、という式について最小二乗法を行っている。
- ここでは両方とも電場の反射率である。光の強度反射率が電場の反射率の2乗になる理由は[1]参照
- については入力ファイルの値(単位が%)を100で割って用いる。
- は
- のようにp波とs波の平均値で与えられる。詳細は詳細02
- また、各はフレネルの公式
- ,
によって求まる。公式の詳細は[1]を参照。
- ここで、はスネルの法則によって計算される。公式の詳細は[1]を参照。
- また、は入力として与えられる定数である。
- したがって、はの関数になっている。
- それでは、は最初どのように与えられるのかについて詳しく述べる。
- 入力の⑪がNOの場合、つまりパラメータを自動で与えるとした場合をまず説明する。
- 最初、のつまりローレンツ関数1つで表せるとしてフィッティングを行う。
- について初期をそれぞれ与える。
- は吸収がない場合の屈折率の値である。コーシーの方程式によって近似的に求めることができるので、物質及び解析範囲に合わせてパラメータとを用いて適切な値を各自計算して、入力⑨として与えてほしい。
- は15とする。これは参考文献[2][2]から、は15付近であるという傾向がわかっているからだ。
- は7.5とする。これは参考文献[2][2]から、との間にという関係があり、さらにが0.5付近の値を多くとるということがわかっているからだ。
- 最後にについてこれは入力④で与えられた解析範囲において入力⑤で読み込みを指定した列の反射率が最小になるところとしている。これはローレンツ関数を実部と虚部に分けたとき、となり、虚部が吸収を表すことが関係している。虚部において最大になるところこそがであり、この時吸収は最大である。これは反射が最小に対応する。ゆえにこのように与えている。屈折率の虚部が吸収を表すことは詳細03で説明している。
1つずつ与える。
- 最小二乗法を行う際、パラメータの範囲はそれぞれは-200から200。入力④で与えられた範囲。は0から500で行っている。
- 最小二乗法が終了すると、残差が求まる。これは、求まったパラメータをに代入する。
- その後、この残差を入力④で与えられた解析範囲の波数の個数で割り、それに対する正の平方根を計算する。これは今後、解析を続けるか結果を返すかの指標になっている。
- これが入力の⑩で与えられた値より小さければ結果を返す。
- 大きければ、ローレンツ関数を1つ増やす。この時、1つ目の初期値は今回の最小二乗法で求まった値を用いる。
- 2つ目の初期値の作り方を説明する。これは、1つ目のローレンツ関数を用いて計算される をから引いた値計算する。この差の関数のうち絶対値が最も大きい値に対応する波数を2つ目のの初期値として与える。絶対値が最も大きな点が極大値の場合と極小値の場合の2パターンがある。模式的に示すと以下のようになる。
- の大きさは1つ目で求まったAの半分としている。これは屈折率の分散の概形が一つ目で与えられていると考え、足りない部分を補うという考えから、一つ目のAより小さいと考えたためである。今回はAの符号も検討する必要がある。これは、差の値が入力ファイルのように反射率が下に凸とは限らないからだ。よってνに対応する値が最小値なら正、最大値なら負というように与えている。最小値の場合、正として与えるのは1つ目の時と同じで反射率が最小の時吸収が最大になると考えるからである。逆の場合は、物理的な意味は考えづらいが数学的に符号を反対にすることが妥当だと考えたからである。
- 2回目以降も同じように残差が入力値より小さいかを判定して、小さければ結果を返し、大きければ1つ増やして、初期値を与えて、最小二乗法行う。これを結果が出るまで繰り返す。2回目以降の残差が大きかった場合の初期値の与え方は1回目と同じである。求まったパ:ラメータから計算される をから引いた値計算する。このうち絶対値が最も大きい値に対応する波数を2つ目のの初期値として与える。の大きさは1つ目で求まったの半分としている。これは屈折率の分散の概形が一つ目で与えられていると考え、足りない部分を補うという考えから、一つ目のAより小さいと考えたためである。の符号はに対応する値が最小値なら正、最大値なら負というように与えている。
- ここまで、入力の⑪がNOの場合の説明をしてきた。次に、入力の⑪がYESの場合の説明をしよう。
- これは、NOの場合とほとんど変わらない。変わるのは、最初の初期値が入力値を採用するということだけである。そのほかの、残差を求めて、それが十分小さくなるまでローレンツ関数を増やしながら、最小二乗法を繰り返すのは同じである。


![{\displaystyle [\left|r\right\vert _{calc}^{2}-\left|r\right\vert _{exp}^{2}]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8609d22abc4838cd2d54b5110c7859ca6692cd98)