「詳細01」の版間の差分
ナビゲーションに移動
検索に移動
タグ: 差し戻し済み |
|||
| (同じ利用者による、間の15版が非表示) | |||
| 1行目: | 1行目: | ||
<div id="詳細01" style="font-size: 150% | <div id="詳細01" style="font-size: 150%;">01:ローレンツ関数を使う理由</div> | ||
: これには2つ理由がある。 | : これには2つ理由がある。 | ||
: 1つはローレンツ関数がクラマースクロニッヒの関係を満たすことだ。 | : 1つはローレンツ関数がクラマースクロニッヒの関係を満たすことだ。 | ||
: 屈折率の実部と虚部がクラマースクロニッヒの関係を満たすことからフィッティング関数にもこのような性質が要求される。 | : 屈折率の実部と虚部がクラマースクロニッヒの関係を満たすことからフィッティング関数にもこのような性質が要求される。 | ||
: この関係式は以下のようなものである。導出は複素積分を使う数学的なものなので導出等は省略する。詳細は参考文献[1]を参照してほしい。<ref name = "ref1" / | : この関係式は以下のようなものである。導出は複素積分を使う数学的なものなので導出等は省略する。詳細は参考文献[1]を参照してほしい。<ref name = "ref1" /> | ||
: <math>n_{1}(\nu) - 1 = \frac{2}{\pi}P\int_{0}^{\infty}\frac{n_{2}(\nu')}{\nu'^2 - \nu'^2}\, d\nu'</math> | : <math>n_{1}(\nu) - 1 = \frac{2}{\pi}P\int_{0}^{\infty}\frac{n_{2}(\nu')}{\nu'^2 - \nu'^2}\, d\nu'</math> | ||
: <math>n_{2}(\nu) = - \frac{2}{\pi}P\int_{0}^{\infty}\frac{n_{1}(\nu')}{\nu'^2 - \nu^2}\, d\nu'</math> | : <math>n_{2}(\nu) = - \frac{2}{\pi}P\int_{0}^{\infty}\frac{n_{1}(\nu')}{\nu'^2 - \nu^2}\, d\nu'</math> | ||
: これが1つ目の理由である。 | : これが1つ目の理由である。 | ||
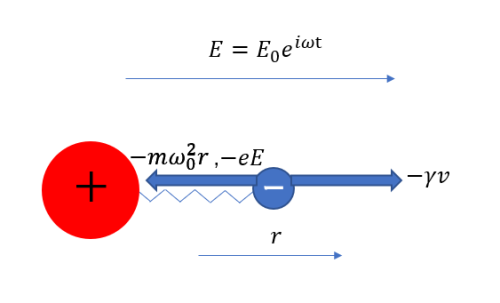
: | : 2つ目の理由は赤外光による振動電場に対する応答がローレンツモデルによってよく表せることが背景になっている。ローレンツモデルでは誘電体の振動電場への応答を正電荷を持つ骨格に電子がばねでつながっている振動子に近似している。模式図は以下のようになる。 | ||
[[File:ローレンツ.png|500px]] | |||
: ここで、<math>m</math>:電子の有効質量、<math>{\omega}_0 = \sqrt{\frac{k}{m}}</math>:振動子の固有振動数、<math>k</math>:ばね定数、<math>\gamma</math>:速度に比例する抵抗である。 | |||
: | : この時以下のような運動方程式が立てられる。 | ||
: <math> m\frac{\partial^2 r}{\partial t^2} + m{\gamma}\frac{\partial r}{\partial t} + m{\omega}_0^2r = -eE</math> | |||
: <math>{\ | : ここでは、導出は省略して最終的に導かれる式のみを示す。詳細は参考文献[2]<ref name = "ref2" />を参照してほしい。 | ||
: | : ローレンツモデルの考え方に基づくと誘電率は以下のように表せる。 | ||
: <math>\hat{\epsilon} = {\epsilon}_{0}\left \{1 + \frac{{\omega}_p^2}{({\omega}_0^2 - {\omega}^2) + i{\omega}{\gamma}} \right \}</math> | |||
: ここで、<math>{\omega}_p = \frac{ne^2}{m{\epsilon}_0}</math>(<math>n</math>単位体積当たりの双極子モーメントの個数。) | |||
: このことから誘電率<math>\epsilon</math>はローレンツ関数で近似的に表されることがわかる。 | |||
: さらに、誘電率<math>\epsilon</math>と屈折率<math>n</math>の間には | : さらに、誘電率<math>\epsilon</math>と屈折率<math>n</math>の間には | ||
: <math>\sqrt{\epsilon} = n</math> | : <math>\sqrt{\epsilon} = n</math> | ||
2021年12月13日 (月) 07:18時点における最新版
01:ローレンツ関数を使う理由
- これには2つ理由がある。
- 1つはローレンツ関数がクラマースクロニッヒの関係を満たすことだ。
- 屈折率の実部と虚部がクラマースクロニッヒの関係を満たすことからフィッティング関数にもこのような性質が要求される。
- この関係式は以下のようなものである。導出は複素積分を使う数学的なものなので導出等は省略する。詳細は参考文献[1]を参照してほしい。[1]
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_{1}(\nu) - 1 = \frac{2}{\pi}P\int_{0}^{\infty}\frac{n_{2}(\nu')}{\nu'^2 - \nu'^2}\, d\nu'}
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_{2}(\nu) = - \frac{2}{\pi}P\int_{0}^{\infty}\frac{n_{1}(\nu')}{\nu'^2 - \nu^2}\, d\nu'}
- これが1つ目の理由である。
- 2つ目の理由は赤外光による振動電場に対する応答がローレンツモデルによってよく表せることが背景になっている。ローレンツモデルでは誘電体の振動電場への応答を正電荷を持つ骨格に電子がばねでつながっている振動子に近似している。模式図は以下のようになる。
- ここで、構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m} :電子の有効質量、構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle {\omega}_0 = \sqrt{\frac{k}{m}}} :振動子の固有振動数、構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle k} :ばね定数、構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \gamma} :速度に比例する抵抗である。
- この時以下のような運動方程式が立てられる。
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle m\frac{\partial^2 r}{\partial t^2} + m{\gamma}\frac{\partial r}{\partial t} + m{\omega}_0^2r = -eE}
- ここでは、導出は省略して最終的に導かれる式のみを示す。詳細は参考文献[2][2]を参照してほしい。
- ローレンツモデルの考え方に基づくと誘電率は以下のように表せる。
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \hat{\epsilon} = {\epsilon}_{0}\left \{1 + \frac{{\omega}_p^2}{({\omega}_0^2 - {\omega}^2) + i{\omega}{\gamma}} \right \}}
- ここで、構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle {\omega}_p = \frac{ne^2}{m{\epsilon}_0}} (構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n} 単位体積当たりの双極子モーメントの個数。)
- このことから誘電率構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \epsilon} はローレンツ関数で近似的に表されることがわかる。
- さらに、誘電率構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \epsilon} と屈折率構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n} の間には
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替(最新ブラウザーや補助ツールに推奨): サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \sqrt{\epsilon} = n}
- という関係があるから、屈折率もローレンツ関数で表しやすいと考えられる。
- 以上の2つの理由からフィッティング関数としてローレンツ関数を用いている。