「ComplexRI」の版間の差分

提供: ComplexRI: Manual
ナビゲーションに移動 検索に移動
118行目: 118行目:


  [[#チュートリアル|チュートリアルtopへ]]
  [[#チュートリアル|チュートリアルtopへ]]
==マニュアル==
{|class="wikitable"
! 目次
|-
|[[#入力01|入力01]]：タイトル
|-
|[[#入力02|入力02]]：ファイル
|-
|[[#入力03|入力03]]：反射率か吸光度か？
|-
|[[#入力04|入力04]]：波数範囲
|-
|[[#入力05|入力05]]：データの列の指定
|-
|[[#入力06|入力06]]：昇順か降順か？
|-
|[[#入力07|入力07]]：実験で用いた基質の種類
|-
|[[#入力08|入力08]]：入射角
|-
|[[#入力09|入力09]]：吸収がないときの屈折率
|-
|[[#入力10|入力10]]：残差の指定
|-
|[[#入力11|入力11]]：フィッティング関数のパラメータの設定の有無
|}
<span id="入力01"  style="font-size: 150%; color:Aqua;">チュートリアル01：タイトル</span>
<span id="入力02"  style="font-size: 150%; color:Aqua;">チュートリアル02：タイトル</span>
<span id="入力03"  style="font-size: 150%; color:Aqua;">チュートリアル03：タイトル</span>
<span id="入力04"  style="font-size: 150%; color:Aqua;">チュートリアル04：タイトル</span>
<span id="入力05"  style="font-size: 150%; color:Aqua;">チュートリアル05：タイトル</span>
<span id="入力06"  style="font-size: 150%; color:Aqua;">チュートリアル06：タイトル</span>
<span id="入力07"  style="font-size: 150%; color:Aqua;">チュートリアル07：タイトル</span>
<span id="入力08"  style="font-size: 150%; color:Aqua;">チュートリアル08：タイトル</span>
<span id="入力09"  style="font-size: 150%; color:Aqua;">チュートリアル09：タイトル</span>
<span id="入力10"  style="font-size: 150%; color:Aqua;">チュートリアル10：タイトル</span>
<span id="入力11"  style="font-size: 150%; color:Aqua;">チュートリアル11：タイトル</span>
[[#マニュアル|マニュアルtopへ]]


==内部処理==
==内部処理==
137行目: 181行目:
: 屈折率の分散をパラメータを使って表したい。ローレンツ関数<math>\frac{A}{\nu_l-\nu-i\gamma}</math>の重ね合わせによって<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>のように表せると考えている。理由は<u>[[#詳細01|詳細01]]</u>参照。
: 屈折率の分散をパラメータを使って表したい。ローレンツ関数<math>\frac{A}{\nu_l-\nu-i\gamma}</math>の重ね合わせによって<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>のように表せると考えている。理由は<u>[[#詳細01|詳細01]]</u>参照。
: 光の強度反射率について最小二乗法を行ってパラメータを決める。つまり、<math>[\left | r \right \vert_{calc}^2 - \left | r \right \vert_{exp}^2]^2</math>という式について最小二乗法を行っている。
: 光の強度反射率について最小二乗法を行ってパラメータを決める。つまり、<math>[\left | r \right \vert_{calc}^2 - \left | r \right \vert_{exp}^2]^2</math>という式について最小二乗法を行っている。
: ここでrは両方とも電場の反射率である。光の強度反射率が電場の反射率の2乗になる理由は<u>[[#詳細02|詳細02]]</u>参照
: ここでrは両方とも電場の反射率である。光の強度反射率が電場の反射率の2乗になる理由は<ref name = "ref2">参照
: <math>\left | r \right \vert_{exp}</math>については入力ファイルの値(単位が%)を100で割って用いる。
: <math>\left | r \right \vert_{exp}</math>については入力ファイルの値(単位が%)を100で割って用いる。
: <math>\left | r \right \vert_{calc}^2</math>は<math>\frac{\left | r^s \right \vert_{calc}^2 + \left | r^p \right \vert_{calc}^2}{2}</math>
: <math>\left | r \right \vert_{calc}^2</math>は<math>\frac{\left | r^s \right \vert_{calc}^2 + \left | r^p \right \vert_{calc}^2}{2}</math>
: のようにp波とs波の平均値で与えられる。詳細は<u>[[#詳細03|詳細03]]</u>
: のようにp波とs波の平均値で与えられる。詳細は<u>[[#詳細02|詳細02]]</u>
: また、各<math>r</math>はフレネルの公式
: また、各<math>r</math>はフレネルの公式
: <math>r_s=\frac{n_1\cos{\theta}_i -n_2\cos{\theta}_t}{n_1\cos{\theta}_i +n_2\cos{\theta}_t}</math>, <math>r_p=\frac{n_2\cos{\theta}_i -n_1\cos{\theta}_t}{n_2\cos{\theta}_i +n_1\cos{\theta}_t}</math>
: <math>r_s=\frac{n_1\cos{\theta}_i -n_2\cos{\theta}_t}{n_1\cos{\theta}_i +n_2\cos{\theta}_t}</math>, <math>r_p=\frac{n_2\cos{\theta}_i -n_1\cos{\theta}_t}{n_2\cos{\theta}_i +n_1\cos{\theta}_t}</math>
によって求まる。公式の詳細は<u>[[#詳細04|詳細04]]</u>を参照。
によって求まる。公式の詳細は<ref name = "ref2">を参照。
: ここで、<math>\sin{\theta}_t</math>はスネルの法則<math>n_1\sin{\theta}_i = n_2\sin{\theta}_t</math>によって計算される。公式の詳細は<u>[[#詳細05|詳細05]]</u>を参照。
: ここで、<math>\sin{\theta}_t</math>はスネルの法則<math>n_1\sin{\theta}_i = n_2\sin{\theta}_t</math>によって計算される。公式の詳細は<ref name = "ref2">を参照。
: また、<math>{\theta}_i, n_1</math>は入力として与えられる定数である。
: また、<math>{\theta}_i, n_1</math>は入力として与えられる定数である。
: したがって、<math>\left | r \right \vert_{calc}^2</math>は<math>n_2</math>の関数になっている。
: したがって、<math>\left | r \right \vert_{calc}^2</math>は<math>n_2</math>の関数になっている。
151行目: 195行目:
: 最初、<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>の<math>lmax = 1</math>つまりローレンツ関数1つで表せるとしてフィッティングを行う。
: 最初、<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>の<math>lmax = 1</math>つまりローレンツ関数1つで表せるとしてフィッティングを行う。
: <math>n_j^0, A, \nu_l, \gamma</math>について初期をそれぞれ与える。
: <math>n_j^0, A, \nu_l, \gamma</math>について初期をそれぞれ与える。
: <math>n_j^0</math>は分散がない場合の屈折率の値である。コーシの方程式<math>n = A + \frac{B}{{\lambda}^2} + \frac{C}{{\lambda}^4}</math>によって近似的に求めることができるので、物質及び解析範囲に合わせてパラメータと<math>\lambda</math>を用いて適切な値を各自計算して、入力⑨として与えてほしい。
: <math>n_j^0</math>は吸収がない場合の屈折率の値である。コーシの方程式<math>n = A + \frac{B}{{\lambda}^2} + \frac{C}{{\lambda}^4}</math>によって近似的に求めることができるので、物質及び解析範囲に合わせてパラメータと<math>\lambda</math>を用いて適切な値を各自計算して、入力⑨として与えてほしい。
: <math>\gamma</math>は15とする。これは参考文献[1]<ref name = "ref1">から、<math>\gamma</math>は15付近であるという傾向がわかっているからだ。
: <math>\gamma</math>は15とする。これは参考文献[1]<ref name = "ref1">から、<math>\gamma</math>は15付近であるという傾向がわかっているからだ。
: <math>A</math>は7.5とする。これは参考文献[1]<ref name = "ref1">から、<math>A</math>と<math>\gamma</math>の間に<math>\frac{A}{\gamma} = {\kappa}_{max}</math>という関係があり、さらに<math>{\kappa}_{max}</math>が0.5付近の値を多くとるということがわかっているからだ。
: <math>A</math>は7.5とする。これは参考文献[1]<ref name = "ref1">から、<math>A</math>と<math>\gamma</math>の間に<math>\frac{A}{\gamma} = {\kappa}_{max}</math>という関係があり、さらに<math>{\kappa}_{max}</math>が0.5付近の値を多くとるということがわかっているからだ。
165行目: 209行目:
: ここまで、入力の⑪がNOの場合の説明をしてきた。次に、入力の⑪がYESの場合の説明をしよう。
: ここまで、入力の⑪がNOの場合の説明をしてきた。次に、入力の⑪がYESの場合の説明をしよう。
: これは、NOの場合とほとんど変わらない。変わるのは、最初の初期値が入力値を採用するということだけである。そのほかの、残差を求めて、それが十分小さくなるまでローレンツ関数を増やしながら、最小二乗法を繰り返すのは同じである。
: これは、NOの場合とほとんど変わらない。変わるのは、最初の初期値が入力値を採用するということだけである。そのほかの、残差を求めて、それが十分小さくなるまでローレンツ関数を増やしながら、最小二乗法を繰り返すのは同じである。
: フィッティングの方法を説明する。
: このアプリケーションでは複素屈折率<math>n_j</math>がローレンツ関数<math>\frac{A}{\nu_l-\nu-i\gamma}</math>の重ね合わせによって<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>のように表せると考えている。そこで、<math>A, \nu, \gamma</math>の３つのパラメータを各ローレンツ関数に対して決定する。このアプリケーションではこれらの決定を最小二乗法を用いて行っている。<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>で表せるとしている背景は[[]]を最小してほしい。具体的な与え方は[[#パラメータ詳細|もう少し先]]で説明することにして、まず全体の流れを説明する。
: 最小二乗法は
: <math>[\left | r \right \vert_{calc}^2 - \left | r \right \vert_{exp}^2]^2</math> ----- (1)
: に対して行っている。
: これは実験から得られた反射率とフィッティング関数を用いて計算される反射率の差を最小にすることを意味する。
: ここで<math>\left | r \right \vert_{exp}</math>は入力で与えられた反射率(%)を100で割った値を用いている。
: <math>\left | r \right \vert_{calc}^2</math>は
: フレネルの公式<math>r_s=\frac{n_1\cos{\theta}_i -n_2\cos{\theta}_t}{n_1\cos{\theta}_i +n_2\cos{\theta}_t}</math>
: <math>r_p=\frac{n_2\cos{\theta}_i -n_1\cos{\theta}_t}{n_2\cos{\theta}_i +n_1\cos{\theta}_t}</math>
: から求める。このときの<math>n_2</math>の部分に<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>を用いている。
: <math>n_1, {\theta}_i</math>は解析を行う上では定数となる。
: なぜなら、<math>n_1</math>は入力⑦つまり基質の屈折率を入れ、<math>{\theta}_i</math>は入力⑧の入射角を常に用いるからである。
: <math>{\theta}_t</math>はスネルの法則<math>n_1\sin{\theta}_i = n_2\sin{\theta}_t</math>から計算されるためこれは<math>A, \nu, \gamma</math>の関数である。
: よって、<math>\left | r \right \vert_{calc}^2</math>は<math>A, \nu, \gamma</math>の関数になっている。
: ゆえに、式(1)<math>[\left | r \right \vert_{calc}^2 - \left | r \right \vert_{exp}^2]^2</math>も<math>A, \nu, \gamma</math>の関数になっている。
: この<math>A, \nu, \gamma</math>を色々変えることによって式(1)の最小値を求めることができれば、その時の<math>A, \nu, \gamma</math>から作られるローレンツ関数は<math>n_2</math>、つまり求めたい物質の複素屈折率をよく表せていることになる。
: <span id ="パラメータ詳細">ここから</span>、<math>n_j=n_j^0+\sum_{l=1}^{lmax} \frac{A}{\nu_l-\nu-i\gamma}</math>がどのように与えられるかをもう少し詳しく説明する。
: <math>n_j^0</math>の部分については入力の⑨で与えた値を用いている。これは屈折率がコーシーの方程式<math>n = A + \frac{B}{{\lambda}^2} + \frac{C}{{\lambda}^4}</math>によって近似的に求められることを利用して与える。これは○○を参照してほしい。
<math>\frac{B}{{\lambda}^2}</math>
----
<span id="説明02" style="font-size: 150%; color:Aqua;">説明02:屈折率のバックグラウンド</span>


  [[#内部処理|内部処理topへ]]
  [[#内部処理|内部処理topへ]]
199行目: 218行目:
! 目次
! 目次
|-
|-
|[[#詳細01|詳細01]]：フィッティング方法
|[[#詳細01|詳細01]]：ローレンツ関数を使う理由
|-
|-
|[[#詳細02|詳細02]]：屈折率のバックグラウンド
|[[#詳細02|詳細02]]：p波とs波の平均値で与えられる理由
|-
|}
|[[#詳細03|詳細03]]：屈折率のバックグラウンド
|-
|[[#詳細04|詳細04]]：屈折率のバックグラウンド
|-
|[[#詳細05|詳細05]]：屈折率のバックグラウンド


|}


<div id="証明01" style="font-size: 150%; color:Aqua;">証明01:屈折率のバックグラウンド</div>
<div id="証明02" style="font-size: 150%; color:Aqua;">証明02:屈折率のバックグラウンド</div>


==参考文献==
==参考文献==
<references>
<references>
<ref></ref>
<ref name = "1">論文</ref>
<ref name = "2">遠藤雅守：電磁場の物理学ーその発生・伝搬・吸収・増幅・共振を電磁気学で理解するー</ref>
<references />
<references />


  [http://comp.chem.tohoku.ac.jp/mediawiki/index.php/ComplexRI ComplexRIページtopへ]]
  [http://comp.chem.tohoku.ac.jp/mediawiki/index.php/ComplexRI ComplexRIページtopへ]]

2021年11月28日 (日) 09:05時点における版


概要

本ComplexRIは全反射実験から得られた反射率あるいは吸光度のデータをもとにして媒質の複素屈折率の分散を出力するWebアプリケーションである。 1⃣実験の結果、 2⃣ファイル形式に関する入力、 3⃣実験の条件、 4⃣解析に関する条件 という四つの情報を入力として与えると、解析が行える。

チュートリアル

チュートリアルでは4種類全10個の入力について、実際に解析を行い、その結果をもとに説明する。
目次
チュートリアル01：ファイルを入れて解析する(入力1⃣を与える練習)
チュートリアル02：解析に関する条件を指定する(入力4⃣を与える練習)
チュートリアル03：ファイルの形式を変える(入力2⃣を与える練習)
チュートリアル04：実験条件を正しく与える(入力3⃣を与える練習)
チュートリアル01：ファイルを入れて解析してみよう➡チュートリアル01の解説へ
ここでは1⃣実験の結果を入力として与えて解析結果を出力させてみよう。
実験結果のファイルはComplexRIのMANUALページのFile Listからダウンロードできる。

MANUAL.png

今回はDownload the File01のボタンを押してダウンロードしてこれを使用してほしい。

FILE DL1.png

ダウンロードが出来たらLSRページに行きファイルを入れてみよう。

LSR.png

入力は①から⑩の10個だ。今回は②Fileにダウンロードしたファイルを与えるだけでFよい。
それではexecute LSRボタンをクリックして解析してみよう。
チュートリアル01の解説
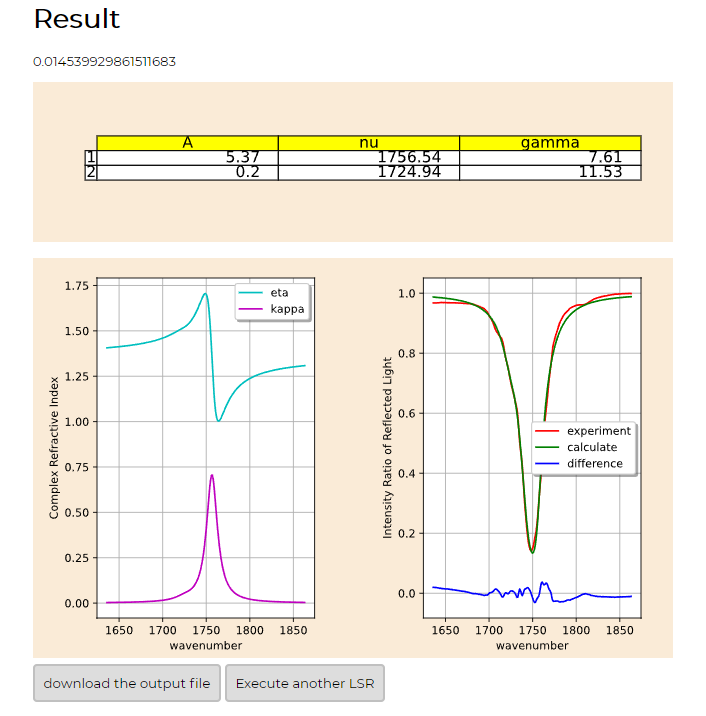
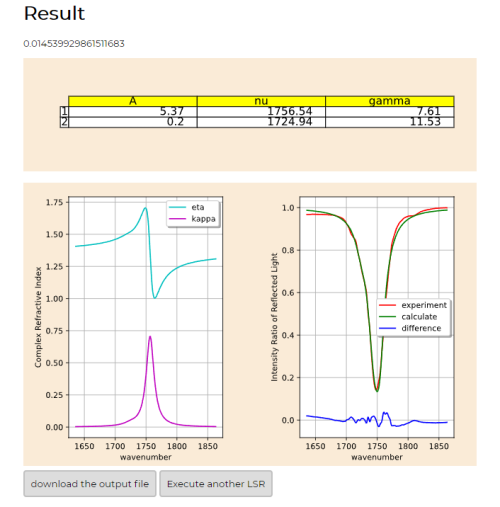
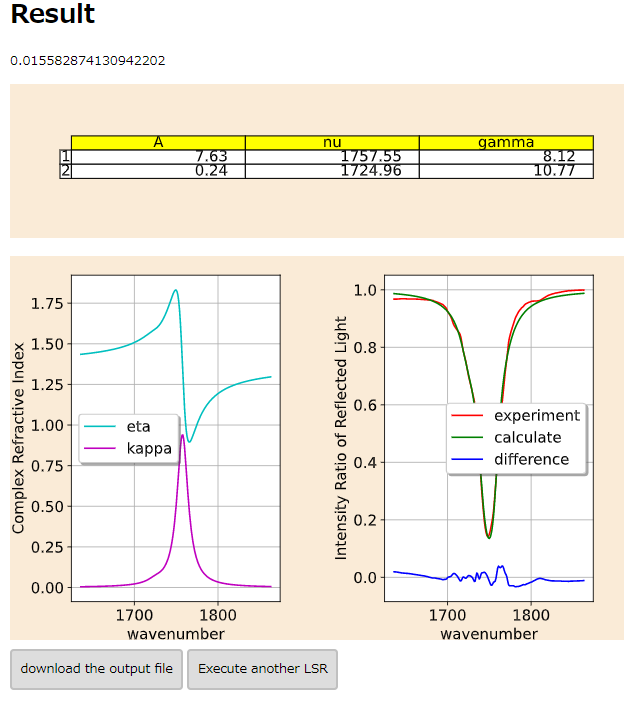
解析結果は以下の画像のようなったはずである。
[図1-1]

caption

ここまでComplexRIの基本的な流れを体験してもらった。
ここで入れたファイルについて簡単に説明する。
この様になっているはずである。

caption

一列目には波数、二列目に一列目の波数の光が入射した時の反射率が(％)単位が並んだ構成になっている。
この様に解析に必要な実験結果は波数とそれに対応する反射率の二種類だけであり、これだけの実験結果から解析が行えるということである。
結果については次のチュートリアルで説明する。
チュートリアル02：解析に関する条件を指定しよう➡チュートリアル02の解説へ
ここでは4⃣解析に関する条件を入力として与えてみよう。
まず、先程と同様にLSRページに行き②Fileにファイルを与える。これは前回と同じものを使用してほしい。
先程はこれで実行していたが、以下のように④と⑩に追加の設定をしてみよう。

０２入力ー４.png０２入力ー１０.png

それではexecute LSRボタンをクリックして解析してみよう。
チュートリアル02の解説
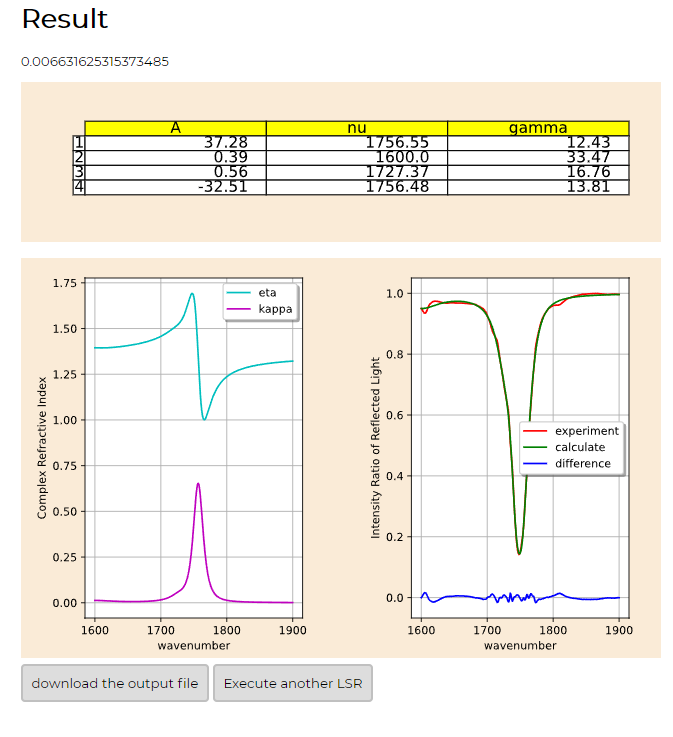
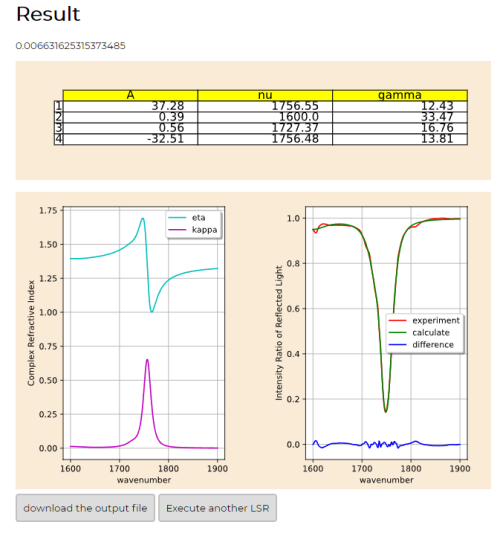
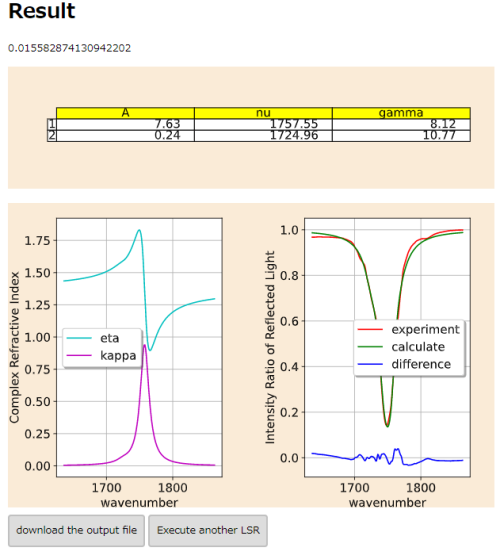
解析結果は以下のようなったはずである。
[図2-1]

caption

④と⑩の入力の意味を説明する前に、結果の見方について簡単に説明する。
(1)数字、(2)表、(3)グラフが並んでいる。
(2)表の数値はフィッティング関数のパラメータである。このフィッティング関数を足し合わせることで、左側の(3)グラフを描いている。また、このグラフの各点の値から反射率を計算してプロットしたのが右側の(3)グラフのcalculateである。実際の回帰ではこの表の数値をいろいろ試して、右側の(3)グラフのcalculateとexperimentと比較するということを行っている。ここで、experimentは入力ファイルとして与えられた反射率の値である。(1)数字は解析が終了した時点で、この比較の差がどれくらい小さくなったかを示している。具体的なフィッティング関数の形や方法については内部処理の説明01：フィッティング方法を参考にしてほしい。
これを踏まえて、④と⑩の入力の意味を説明していこう。
説明は今回の結果をチュートリアル01の時と比較しながら行っていく。
図の比較は以下のようになる。
左がチュートリアル01の結果。右がチュートリアル02➡チュートリアル01の結果を直接見る。の結果。

０１結果.png０２結果.png

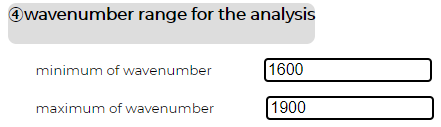
④の入力をしたことは、グラフの横軸の幅を設定することなっている。確かに、[入力4の図]と同じ範囲になっている。デフォルトの値で行われたチュートリアル01の時と比べると変化がわかりやすいと思う。
このグラフの幅の設定は、言い換えると、解析する波数の範囲設定したことになっている。これは直前に説明した解析の原理から考えればわかる。(3)グラフのcalculateとexperimentを比較するのであった。このときグラフの横幅を変えれば、比べる範囲つまり解析の範囲を変えることに相当するということだ。
次に⑩について説明する。今回は[入力１０の図]のように0.01した。解析は(1)数字がこの値より小さくなったら終了するようになっている。つまり解析の正確さもしくは厳しさを設定することになっている。これは小さくしすぎないように注意してほしい。なぜなら、比較の差分がこれよりも小さくならず、解析がとても長くなることがあるからだ。目安としてはデフォルトの0.02から0.01がよい。これは適宜試してみてほしい。
チュートリアル03：ファイルの形式を変えてみよう➡チュートリアル03の解説へ
ここでは2⃣ファイル形式に関する条件を入力として与えてみよう。
チュートリアル01の時と同様にMANUALページのFile Listからファイルをダウンロードしてほしい。
今回はFile02を使う。

FILE DL2.png

ダウンロード出来たら、LSRページに行き②Fileにファイルを与える。
今回は③，⑤，⑥の入力を以下のように変更してみよう。

０３入力ー３.png０３入力ー５.png０３入力ー６.png

それではexecute LSRボタンをクリックして解析してみよう。
チュートリアル03の解説
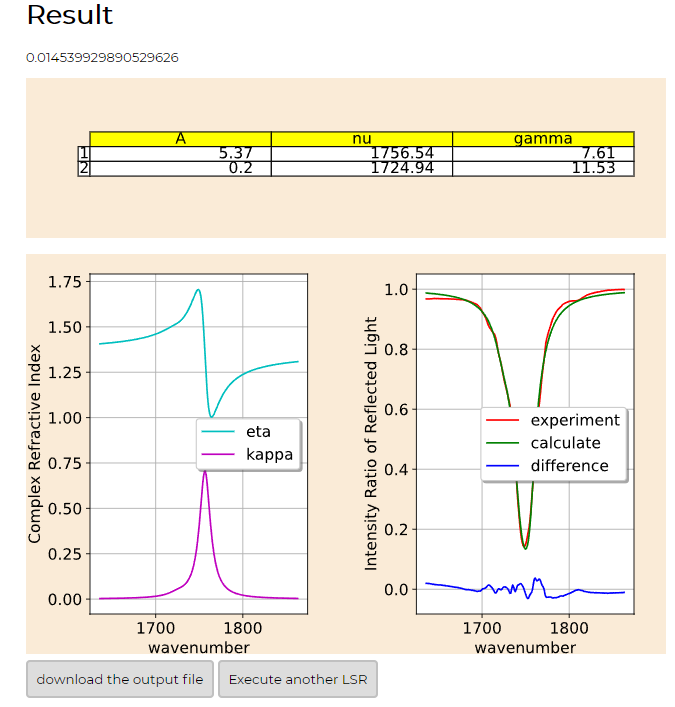
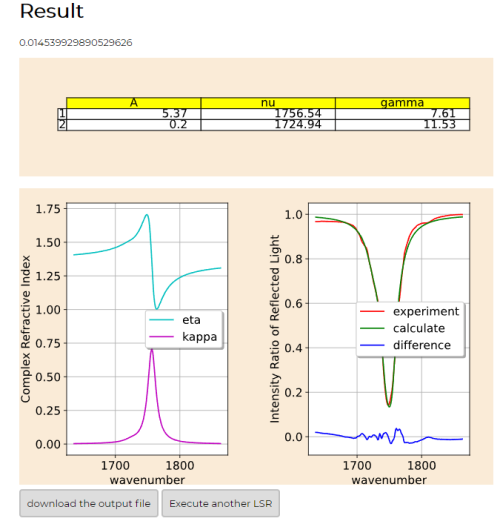
解析結果は以下のようなったはずである。

caption

じつはこれはチュートリアル01と同じ結果になっている。
左がチュートリアル01の結果。右がチュートリアル03の結果。➡チュートリアル01の結果を直接見る。

０１結果.png０３結果.png

これは全く同じになっている。
これは同じ実験結果を入力したことを意味している。しかし、チュートリアル01と02で使用した入力ファイルと今回使用した入力ファイルを比較すると、以下のように一見同じには見えない。これが同じであることを説明する。（一部分のみ示す。）
左がチュートリアル01の入力ファイル。右がチュートリアル02の入力ファイル。

captioncaption

異なる点は２つある。
1つは行が3行になっていることである。これは波数、反射率、吸光度の順に並んでいる。ここで新しく出てきた吸光度というのは反射率と等価な情報を表している。なぜなら、(証明)という関係式が成り立っており、これによって吸光度を反射率に変換することができるからだ。
もう1つは波数と反射率の並びが昇順から降順になっていることだ。ここで、吸光度はこの様に並び替えた後で反射率から計算したので波数に対応している。
このように形は異なるが等価な実験結果を与えた。だから結果が同じだったのだ。
③，⑤，⑥の入力はこのファイルの形の違いをアプリ側に考慮させるために入力した。
⑤では読み込む列の番号を与えたことになっている。今回は入力として1行目の波数と3行目の吸光度を使うのでこのように設定した。
吸光度を使うときは、忘れずに③をabsorptanceに設定してほしい。すると、解析時に反射率に変換して解析する。
この設定はデフォルトではreflectanceになっているのでこれまでは変更する必要がなかった。
最後に⑥はデータの波数のの並び方昇順か降順かを入力している。今回は降順なのでこのように設定した。デフォルトは昇順なので今までは設定する必要がなかった。
チュートリアル04：実験条件を変えてみよう➡チュートリアル04の解説へ
ここでは3⃣実験の条件を入力として与えてみよう。
LSRページに行き②Fileにファイルを与える。これはチュートリアル01と02で使ったものと同じものを使ってほしい。
今回は⑦，⑧，⑨の入力を以下のように変更してみよう。

caption

それではexecute LSRボタンをクリックして解析してみよう。
チュートリアル04の解説
解析結果は以下のようなったはずである。

caption

チュートリアル01とグラフを比較してみると以下のようになる。
左がチュートリアル04の結果。右がチュートリアル01の結果。➡チュートリアル01の結果を直接見る。

０４結果.png０１結果.png

同じファイル、つまり同じ実験結果を与えているが、実験条件が違えば、出力も異なることがわかる。正しい分散を求めるには自身の行った実験の条件を正しく与える必要があるということだ。
各入力を説明しよう。
⑦では全反射実験のときに使った基質の種類を指定している。
⑧では全反射実験のときの入射光の角度を指定している。
⑨では分散のバックグラウンドを与えている。これは測定する基質の赤外領域での屈折率を与える必要がある。
これは可視光領域の光に対する屈折率からコーシの方程式のパラメータを求め、これを外挿することによって求めることができる。
詳しい求め方は内部処理の説明02：屈折率のバックグラウンドを参考にしてほしい。
チュートリアルtopへ

マニュアル

目次
入力01：タイトル
入力02：ファイル
入力03：反射率か吸光度か？
入力04：波数範囲
入力05：データの列の指定
入力06：昇順か降順か？
入力07：実験で用いた基質の種類
入力08：入射角
入力09：吸収がないときの屈折率
入力10：残差の指定
入力11：フィッティング関数のパラメータの設定の有無

チュートリアル01：タイトル チュートリアル02：タイトル チュートリアル03：タイトル チュートリアル04：タイトル チュートリアル05：タイトル チュートリアル06：タイトル チュートリアル07：タイトル チュートリアル08：タイトル チュートリアル09：タイトル チュートリアル10：タイトル チュートリアル11：タイトル 



マニュアルtopへ

内部処理

目次
説明01：フィッティング方法
説明02：屈折率のバックグラウンド
説明03
説明04

説明01:フィッティング方法

屈折率の分散をパラメータを使って表したい。ローレンツ関数の重ね合わせによってのように表せると考えている。理由は詳細01参照。
光の強度反射率について最小二乗法を行ってパラメータを決める。つまり、という式について最小二乗法を行っている。
ここでrは両方とも電場の反射率である。光の強度反射率が電場の反射率の2乗になる理由は引用エラー: <ref> タグに対応する </ref> タグが不足しています

引用エラー: 無効な <ref> タグです。名前に単なる整数は使用できません。説明的なものにしてください 


ComplexRIページtopへ]
「http://comp.chem.tohoku.ac.jp/mediawiki/index.php?title=ComplexRI&oldid=345」から取得