「出力」の版間の差分
ナビゲーションに移動
検索に移動
| 5行目: | 5行目: | ||
: 式にすると<math>\sum_{{\nu}\in[{\nu}_{min},{\nu}_{mmax}]} ([\left | r(\nu) \right \vert_{calc}^2 - \left | r(\nu) \right \vert_{exp}^2]^2)</math>である。 | : 式にすると<math>\sum_{{\nu}\in[{\nu}_{min},{\nu}_{mmax}]} ([\left | r(\nu) \right \vert_{calc}^2 - \left | r(\nu) \right \vert_{exp}^2]^2)</math>である。 | ||
: 結果で表示している値はさらにこの値を解析範囲の波数の個数で割り、その平方根をとったものとなっている。つまり、標準偏差である。 | : 結果で表示している値はさらにこの値を解析範囲の波数の個数で割り、その平方根をとったものとなっている。つまり、標準偏差である。 | ||
: 式にすると、<math>\sqrt{\ | : 式にすると、<math>\sqrt{\sum_{{\nu}\in[{\nu}_{min},{\nu}_{mmax}]} ([\left | r(\nu) \right \vert_{calc}^2 - \left | r(\nu) \right \vert_{exp}^2]^2)}{N_{\nu}}}</math>(※<math>N_{\nu}</math>は解析範囲の波数の個数) | ||
: このような値を用いる理由は解析範囲によらず最小二乗誤差の値を評価するためである。 | : このような値を用いる理由は解析範囲によらず最小二乗誤差の値を評価するためである。 | ||
---- | ---- | ||
2021年12月2日 (木) 01:00時点における版
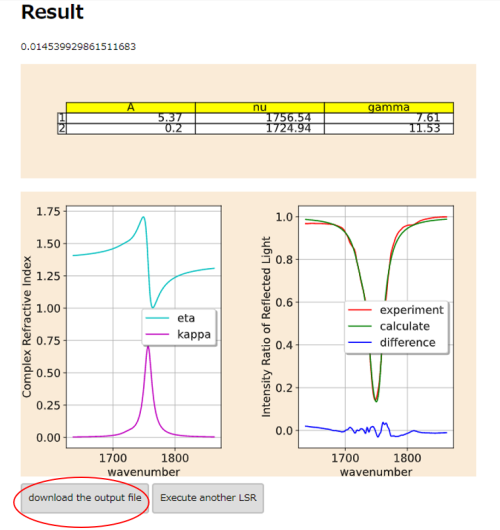
01：数値
- これは解析終了時の最小二乗誤差に比例した量になっている。これが小さいほどパラメータを使って表された屈折率の分散が実際の分散の様子に近いことを意味する。
- 数値についてもう少し詳しく説明する。
- まず最小二乗誤差は入力ファイルで与えられた反射率の値からパラメータによって表された屈折率によって計算される反射率を解析範囲の各波数において引き算して、この結果をそれぞれ二乗してその和をとったものである。
- 式にするとである。
- 結果で表示している値はさらにこの値を解析範囲の波数の個数で割り、その平方根をとったものとなっている。つまり、標準偏差である。
- 式にすると、構文解析に失敗 (構文エラー): {\displaystyle \sqrt{\sum_{{\nu}\in[{\nu}_{min},{\nu}_{mmax}]} ([\left | r(\nu) \right \vert_{calc}^2 - \left | r(\nu) \right \vert_{exp}^2]^2)}{N_{\nu}}}} (※は解析範囲の波数の個数)
- このような値を用いる理由は解析範囲によらず最小二乗誤差の値を評価するためである。
![{\displaystyle \sum _{{\nu }\in [{\nu }_{min},{\nu }_{mmax}]}([\left|r(\nu )\right\vert _{calc}^{2}-\left|r(\nu )\right\vert _{exp}^{2}]^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e485d77fef825fac9aa17116263b0d5865fe57f)
02：表
- これはフィッティング関数（ローレンツ関数）の各パラメータである。
- 各行は1つのローレンツ関数に対する一組のパラメータを表している。
03：グラフ
- 3つのグラフがプロットされると思う。
- experimentとあるのは入力ファイルで与えられた光の強度反射率を解析範囲の波数に対してプロットしたものである。
- calclateとあるのは パラメータを使って表された屈折率をもとに計算された光の強度反射率を解析範囲の波数に対してプロットしたものである。
- differenceはcalclateからexperimentを引いた値をプロットしたものである。
04：ファイル
- これは以下のボタンを押すとダウンロードすることができる。
- これには上記にあるような数値、表、グラフのほかにグラフの各点での値などが載せてある。