1.  理論・計算化学による凝縮系の化学過程の研究

1.1 研究の背景と目的[1]　

　化学反応の経路を理論、計算化学の手法によって決定することは、理論化学のみならず物理化学における最も重要な課題の１つである。 よく知られているように、気相における少数の原子からなる系の化学過程の理論的研究は、1930年代にEyringらによって構築された遷移状態理論にまで遡る。これは、活性錯合体と反応物との間に平衡状態が成り立つという仮定のもとにつくられた極めて強力な統計力学の理論である。この理論では、反応速度は反応物や活性錯合体の分子分配関数、ひいてはそれら分子の基準振動の振動数、電子状態のエネルギーといった分子固有の性質によって記述される。従って、この理論が使い物になるためには、すなわち、これによって反応の経路や速度を先見的に予測することが可能となるためには、それに続く量子化学計算の方法論の開発と計算機の進歩とを待たねばならなかった。実際、この理論が、パッケージ化された量子化学計算ソフトによって、理論家のみならず実験家もが普通に使うツールにまでなったのは、ほんのこの10年ぐらいのことである。今や信じられないことだが、文献[2]の序文には、1960年代には、研究者の多くがこの理論の将来に全く悲観的であったことを伺わせるエピソードが紹介されている。当時、電子状態を決定するための有効な方法がなく、そもそも遷移状態の構造を決定することすらできなかったということがその主な原因である。

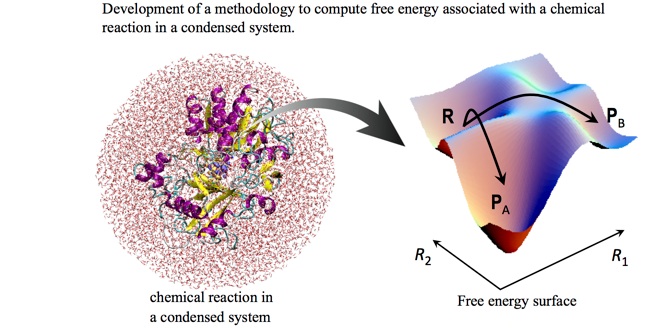
　こうした事情を背景にして、化学反応の理論研究の場を気相から、溶液や生体分子のような実在系へと拡張しようとする研究が、現在、盛んに行われている。しかし、凝縮系の化学過程を理論的に記述する上で、大きな足かせが２つある。１つは、化学反応を記述するには、言うまでも無く量子化学的な手法が必須であり、多粒子系の第一原理計算を行う必要があるということである。 量子化学計算では、最も安価な手法でも、その計算コストは、系に含まれる電子数の３〜４乗に比例するので、多粒子の電子状態をいかに効率良く決定するかという問題は深刻である。もう１つの問題は、凝縮系の反応経路を支配する量である自由エネルギー変化をいかに計算するかということである。 我々の主な興味の対象である溶液や生体系では、それを構成する原子、分子の熱的な運動が顕著であり、エントロピーの影響が無視出来ない。現在、古典力学をベースとする分子シミュレーションでは、計算機の性能のおかげで数千から数万の粒子を扱うことが普通になっているが、自由エネルギーの計算は依然として困難な問題として知られている。おもな原因は、それが、ある１つのアンサンブルの平均によっては、計算できないという事実にある。数値的に厳密なアプローチとしては、反応の始状態と終状態を結ぶ任意の経路に沿って、多数の中間状態を取り、これらの状態間の自由エネルギー差を積分するという方法がある。これは、経路に沿って多数のアンサンブルを発生させるので、当然、大きな計算コストが必要となる。

　筆者らが目的とするのは、凝縮（実在）系の反応経路を先見的に予測するための理論・計算化学上の方法論を開発し、それを具体的な興味ある系に応用することである。詳細は以下の章に譲るが、筆者らが擁する方法論の具体的な枠組みは、前段の２つの課題に対応して、第一原理の方法としてはハイブリッド型の第一原理分子動力学法（QM/MM）法[3]であり、自由エネルギー計算の方法としては新規な溶液の理論であるエネルギー表示の理論[4]についてである。上でも述べたように、自由エネルギーは、反応経路を決定する上で最も重要な物理量である。また、それ故にいかなる物理化学の教科書にも載っている平凡な概念でもある。しかし、それを分子論に基づく計算によって決定するのは全く容易ではない。 量子化学の分野では、凝縮系の計算に対しては、ある与えられた構造の一点の電子状態が決定されれば、それがゴールであって、自由エネルギーはどちらかと言うと瑣末な問題とする傾向があるように感ずる。筆者の杞憂かも知れないが、これは無論、正当ではない。

　科学上の方法において、筆者が重要視するのは、方法論の形式の簡潔性や、その出発点となるモデルの明瞭性である。 モデルの明瞭性とは、そのモデルの物理的内容が単純でwell-definedであること、と言い換えられる。汎用（一般）性のある優れたモデルほど簡潔であることは、我々が経験によって良く知るところである。卑近な例では、分子軌道法における独立粒子モデルや、電子密度汎関数法における局所密度近似(LDA)などがある。これらの方法はあまりに単純なために実用上、常に軽視されるが、現象の解釈や予測において必須なツールになっている。自然現象が比較的単純なモデルで記述可能であるという経験的事実は方法論の開発の上で重要な指針となりうる。我々がこれまでに開発してきた後述の方法も、それを構成する個々の理論の基本的な枠組みが簡潔であり、それ故に様々な応用に耐える強固な方法となっている。 実際、様々な応用計算によって、我々の方法が従来の方法と比較して、計算精度や効率において優れていることが実証されている。

1.2 方法論の概要　

1.2.1 電子状態計算について　

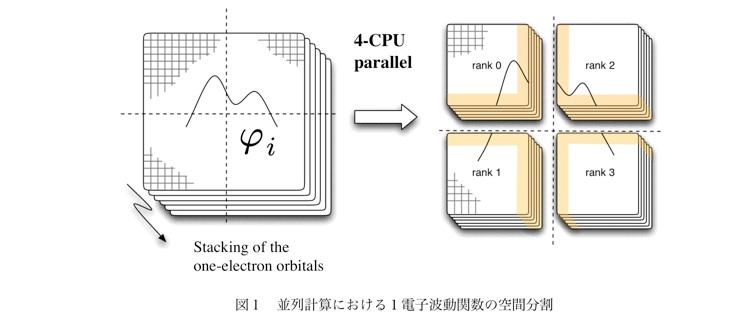
　電子状態計算において、我々が採用したのはKohn-ShamのDFT (KS-DFT) 法である。KS-DFT法は計算コストが小さいわりに精度の高い方法として、既に世界的に確固たる地位を築いている。 では、凝縮系の研究における、KS-DFT法の利点は何か？ KS-DFTでは、電子間の非古典的な相互作用（交換、および相関）を場所 rにおける局所、あるいは準局所な演算子で記述する。これらの演算子は具体的には、電子密度 n(r) やその勾配によって記述される。これが大規模計算において果たす役割は、以下に述べる理由によって、絶大である。計算機の潮流は汎用機からスパコンに至るまで、多数のCPUを高速なネットワークで繋いで構成する並列型に移行しており、この流れは今後も続くと考えられる。次世代スパコンはその代表であり、研究室においても、数百のCPUからなるクラスターは珍しくない。量子化学計算においても超並列計算を指向する方法が望ましい。並列計算では、全系をなんらかの方法で分割し、各ドメインの計算を１つのCPUが担当する。演算子の中に非局所なポテンシャルが含まれているとすると、すべてのCPUが波動関数に関する情報を共有していなければならず、これはCPU間（ノード間）の通信コストの増大をもたらす。演算子が局所的である場合、CPUは他のドメインの波動関数の値を保持する必要はない。従って、DFT法では通信量を最小に抑えることが可能である。 また、DFT法が、CI法のように多数の電子配置から電子相関を構築するよりもはるかに効率的であることは、言うまでもない。

　前段で述べた内容は、無論、波動関数を表現する基底の取り方に依存する。「局所的」と書いたのは、あくまでも実空間上で、という意味である。従って、KS-DFTの利得は、どんな基底を選んでも得られるという訳ではない。一電子波動関数を展開する関数として通常良く用いられるのは、原子基底と平面波である。前者は伝統的に原子、分子のような有限系において、また、後者は結晶やバルク、表面に対して主に用いられてきた。これらに対して、波動関数を実空間上に一様に置かれたグリッド上の確率振幅のセットによって記述する方法が第三の方法として用いられるようになってきた。この基底によれば、KS-DFT法で使われる一電子有効ハミルトニアンの表現行列が実空間において対角優勢になることから、大規模並列計算においてCPU間の通信コストが著しく低減できる。 大規模な並列計算を考えるとき、原子基底による展開では、基底関数間の２電子積分に関わる情報の通信が足かせになり、平面波基底による方法では、一電子波動関数を運動量空間から実空間へ変換する（あるいはその逆変換）時に必要となる多数回の高速フーリエ変換 (FFT) が足かせになることが知られている。これに対して実空間表示においては運動エネルギー演算子やGGA汎関数は準局所な演算子となるので、波動関数を図1のような空間分割によって並列化する場合は、CPU間の通信は極力抑えることが可能である。図において、色付けされた部分は、隣にあるセルとの情報交換が必要な領域である。今後、実空間グリッド法が量子化学の分野において、標準的な手法となる可能性がある。このような事情から、我々は当初より、独自に実空間グリッド法によるKS-DFT法を開発してきた。　この方法は、実時間発展のプログラムへと拡張することも可能であり、結果として凝縮相中の光反応の解析も可能になる。重要なことに、電子状態計算の核としてDFT法を用いる限り上で述べた利点はそのまま適用される。

　

1.2.2 自由エネルギー計算について　

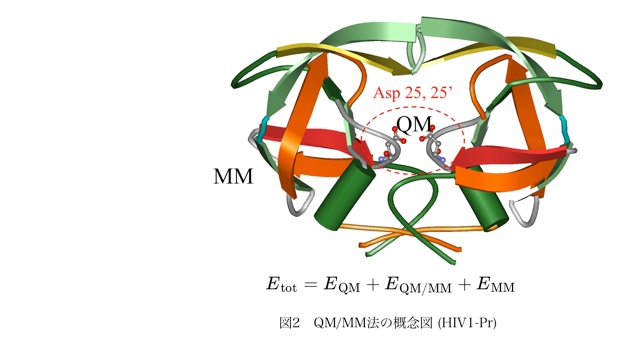
　我々が、多粒子系を研究するために採用した方法として、ハイブリッド型の第一原理分子動力学法 (QM/MM法) がある。この方法の枠組みは単純であり、それ故に、溶液や生体分子など極めて広大な応用分野を持ち、既に多くの応用計算が実施されている。QM/MM法は、全系のうち反応に関与する部分のみを量子化学的に扱い、それ以外の電子的に静的なパートを古典力学の分子力場で記述する(図2)。QM/MM法では、MM系がつくる静電場をQM系のハミルトニアンに加えることにより、環境部位の影響を考慮しながらQM系の電子状態を決定することができる。 QM/MM法は、単に計算コストが小さいというだけではなく、注目する化学的イベントのコアとなる部分とその環境との繋がりを解析する上でも非常に都合が良い、ということは注目されるべきである。また、QM/MM法は、所謂、マルチスケール-マルチフィジックスの単位となる手法であり、多階層からなる分子シミュレーションへと自然に拡張される。

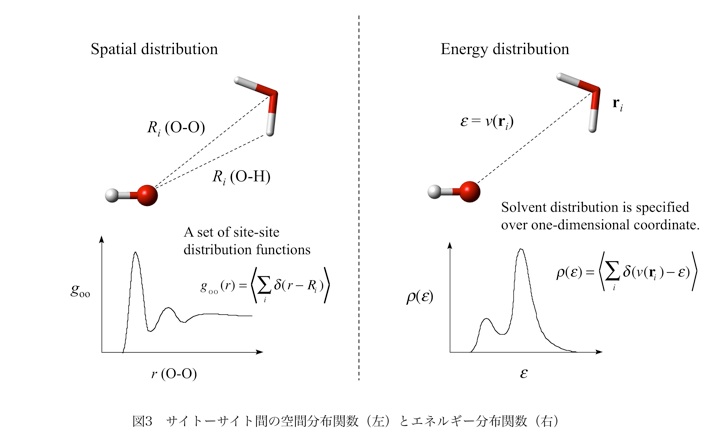
　化学過程に伴う自由エネルギー変化は、熱揺らぎが無視できない系では本質的に重要な物理量である。自由エネルギーを計算する方法として、自由エネルギー摂動法 (FEP) や熱力学的積分法 (TI) などのbrute force的な、数値的に厳密な方法の他に、溶液の分布関数理論（密度汎関数法）による方法がある。上でも述べたように、FEPやTI法はある経路に沿っての溶媒の配置のアンサンブルをシミュレーションによって算出する必要があり、計算コストが大きい。これに対して、溶液論によれば、近似的な汎関数を使う代わりに、始点と終点における溶質周りの溶媒の分布関数のみから自由エネルギーを構築するので、はるかに効率が良い。このようなことから、我々は前述のQM/MM法と溶液論を融合する方法(QM/MM-ER法)を採用している[5]。 具体的には、溶液論として、松林氏の開発したエネルギー表示の理論[4]を用いている。エネルギー表示の理論は、溶質ー溶媒間の相互作用エネルギーの分布関数を基本変数とする分布関数理論であり、従来の空間分布関数に基づく方法には無い優れた特徴を持つ。溶質と溶媒分子がそれぞれ、構造を持つ場合（殆どの場合そうである）、空間分布関数の変数は位置と配向を担う6つの独立変数からなる。これをまともに扱うのは、数値計算上、極めて困難である。従って、通常、分子上に相互作用点を置くことによって、あらわな空間分布関数を相互作用点間の分布関数のセットに縮約する。縮約された分布関数は、当然、もとの分布関数と等価ではあり得ないことに注意されたい。これに対して、エネルギー表示の理論では、高々、１次元のエネルギー分布関数そのものが、密度汎関数法の基本変数として使われるので、正確な分布関数が与えられれば、エラーは近似的汎関数にのみ由来することになる。 量子化学的な方法との結合において、さらに有利なことに、エネルギー表示の理論は人工的な相互作用点を必要としないので、QM系の電子密度を点電荷に縮約する必要がない。

　最近、我々は、エネルギー表示の理論を拡張することによって、QM-MM間の多体の相互作用（電子密度の揺らぎ）に起因する自由エネルギーを計算するための、簡潔かつ、数値的に厳密な方法を開発した[6]。 我々の計算によれば、溶液中で溶質の電子密度が揺らぐことによる自由エネルギーへの寄与は、定量的に全く無視できない。このような多体の効果は、特にアニオンやanionic 分子上のサイトにおいて顕著である。さらに、簡潔な式を得たことで、古典の分極モデルに基づくシミュレーションへの拡張[7]や、多体の自由エネルギーの分解など、種々の解析も可能になった。

1.3 参考文献　

本文中のcitation:

[1]    高橋英明、「QM/MM法と溶液の理論に融合による凝縮系の化学過程の自由エネルギー計算(1)」

          分子シミュレーション研究会会誌「アンサンブル」, Vol. 10, 25 (2008).

[2]    The Transition State, edited by T. Fueno Kodansha, Tokyo, 1999.

[3]    “A hybrid QM/MM method employing real-space grids for QM water in the TIP4P water solvent”,

         H. Takahashi, T. Hori, et al. J. Comp. Chem. 22, 1252 (2001).

[4]    “Theory of solutions in the energetic representation. I. Formulation”,

         N. Matubayasi, et al. J. Chem. Phys. 113, 6070 (2000). 

[5]    “A quantum chemical approach to the free energy calculations in condensed systems: The QM/MM

         method combined with the theory of energy representation”,

         H. Takahashi, N. Matubayasi et al. J. Chem. Phys. 121, 3989 (2004).

[6]    “Simple and exact approach to the electronic polarization effect on the solvation free energy:

         Formulation for quantum mechanical/molecular mechanical system and its applications

         to aqueous solutions”, H. Takahashi et al. J. Chem. Phys. 136, 214503 (2012).

[7]    “Development of a methodology to compute solvation free energies on the basis of the theory of energy

          representation for solutions represented with a polarizable force field”, D. Suzuoka, H. Takahashi, et al.

          J. Chem. Phys. (2012) submitted. 

Reviewなど:

[1]    “Development of a Quantum Chemical Method Combined with a Theory of Solutions:

            Free Energy Calculation for Chemical Reactions by Condensed Phase Simulations”,

            H. Takahashi, N. Matubayasi, et al. Advances in Quantum Chemistry (Elsevier), 59, 283-351 (2010).

[2]     “A quantum chemical approach to free energy calculation for chemical reactions in condensed

            system: Combination of a quantum chemical method with a theory of statistical mechanics”,

            H. Takahashi, N. Matubayasi, et al. Challenges and Advances in Computational Chemistry

            and Physics 6: Solvation Effects on Molecules and Biomolecules (Springer), 455-505 (2008).

2.  電子密度汎関数理論における交換汎関数の開発

　電子の密度汎関数法(DFT)において、定量的な見地から言って、交換汎関数の果たす役割は大きい。現在、利用されているほぼ全ての交換汎関数のベースはLDAであり、これは一様な電子ガスの交換ホールをモデルとしている。LDAのような簡素なモデルが、少なくとも定性的には原子、分子の性質を記述しうるという事実はまさに驚くべきである。しかし、DFTによって、原子、分子について定量的な議論が可能になるのは、ようやくBeckeのGGA汎関数[1]によるLDAに対する補正が確立されてからである。しかしながら、このGGA汎関数は、それが交換ホールそのものに対する具体的なモデルを与えていないという意味においてwell definedではない。 rに置かれた参照電子の周りで電子密度が揺らぐ（勾配を持つ）と交換ホールが収縮し、結果として、rでの交換エネルギー密度が増大する。通常のGGA汎関数は、この揺らぎの効果を再現するように作られた式であり、収縮した交換ホールのモデルを与えるものではない。このような形式は、副作用として好ましくないエラーを発生する。一般的なGGA汎関数のもっとも大きな問題点は、参照点 r を分子の外縁部に遠ざけた時に交換ポテンシャルが急速に減衰するということにある。上に述べた方法では、交換ホールと参照電子とが解離するという描像が原理的に再現できないことがその原因である。LDAを出発点とする近似の体系はバルク固体に対しては適切だが（交換ホールが常に参照電子の近傍に位置するので）、原子、分子に対しては明らかに適切ではない。

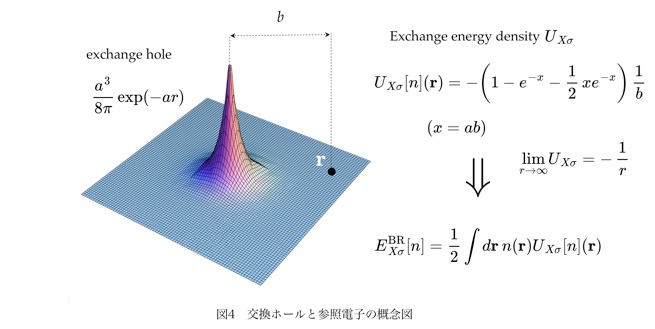
　これに対して、Becke-Roussel(BR)らは、水素様の原子の交換ホールをモデルとする新規な交換汎関数を提案した[2]。このモデルによれば、交換ホールと参照電子の解離が自然に再現される(図4)。従って、交換エネルギー密度やポテンシャルの長距離性が、なんら付加的な工夫を施すことなく実現される。これは、参照電子と交換ホールとの相互作用の長距離性がモデルの中に最初から組み込まれているからであり、それ故に優れた方法と言える。しかし、この方法には、平面波や実空間基底において、変分計算が実行できないという決定的な問題がある。我々は、オリジナルのBR法とは全く異なる手法で、実空間や平面波基底での変分計算を可能にする方法を新規に開発した [3]。 

参考文献：

[1]    “Density-functional exchange-energy approximation with correct asymptotic behavior”, 

           A. D. Becke, Phys. Rev. A. 38, 3098 (1988).

[2]    “Exchange holes in inhomogeneous systems: A coordinate-space model”, A. D. Becke

          and M. R. Roussel, Phys. Rev. A. 39, 3761 (1989).

[3]    “The exchange-energy density functional based on the modified Becke-Roussel model”,

           H. Takahashi et al, J. Chem. Theory Comput. 6, 647 (2010).