Theory
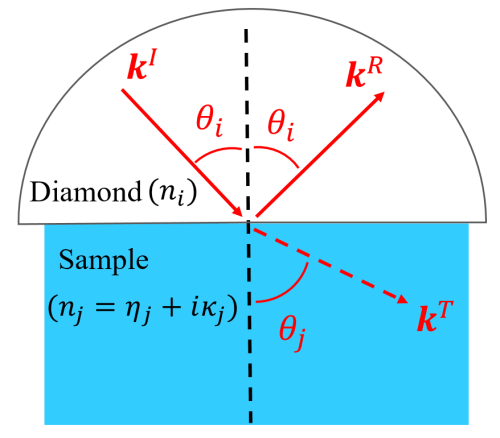
The experimental geometry is described by the two-layer model in the above Figure, where phase 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i} and phase 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle j} represent the substrate and sample, respectively. The incident light in phase 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle i} and transmitted light in phase 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle j} are related by Snell's law
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_i \sin \theta_i = n_j \sin \theta_j }
where 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_i} and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j} are the complex refractive index of substrate and sample. 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \theta_i} and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \theta_j} denote the angles of incidence and transmission of IR light, respectively.
The reflectance of 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle p} - and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle s} -polarized lights can be represented as the ratio of reflected to incident light intensities by [1]
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle | r_{ij}^p|^2 = \left| \frac{n_j \cos \theta_i - n_i \cos \theta_j}{n_j \cos \theta_i + n_i \cos \theta_j} \right|^2 }
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle | r_{ij}^s|^2 = \left| \frac{n_i \cos \theta_i - n_j \cos \theta_j}{n_i \cos \theta_i + n_j \cos \theta_j} \right|^2 }
The angle of transmission 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \theta_j} is derived from Snell's law to be
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \cos \theta_j = \sqrt{1-\frac{n_i^2}{n_j^2} \sin^2 \theta_i} }
which can be imaginary in the ATR condition.
In the experiment, the incident angle 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \theta_i} is often fixed, for example, to 45 degree. Take substate diamond as example, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_i } is also known as 2.38. Therefore, the ATR condition is satisfied in most cases where 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j } is smaller than 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_i \sin \theta_i = 1.68 } . This situation is held for most liquid samples. In the total reflection condition, the calculated 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle | r_{ij}^p|^2 } and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle | r_{ij}^s|^2 } are unity when 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j } is real. However, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle | r_{ij}^p|^2 } and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle | r_{ij}^s|^2 } become less than unity when the refractive index of the liquid 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j = \eta_j + i \kappa_j } is complex. The reduced reflectance is a consequence of the absorption of evanescent light in the liquid sample. Therefore, by fitting the experimental reflectance data in ATR-IR spectra, it is able to obtain the complex refractive index of the liquid sample.
The purpose of fitting is to determine the frequency-dependent complex refractive index 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j(\nu) } . The complex refractive index of sample is represented with a set of Lorentz functions
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j (\nu) = \eta_j (\nu) + i \kappa_j (\nu) = n_j^0 + \sum_{l=1}^{l_\text{max}} \frac{A_l}{\nu_l - \nu - i \Gamma_l} }
where 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j^0 } is the nonresonant refractive index. 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_l } , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \nu_l} and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \Gamma_l} are the amplitude, peak wavenumber and bandwidth of each Lorentz function, respectively. 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle l_\text{max} } is the number of Lorentz functions to be used. Therefore, the parameters 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j^0 } , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_l } , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \nu_l} and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \Gamma_l} and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle l_\text{max} } were determined from the experimental spectra.
In the beginning, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j^0 } should be determined before the fitting procedure. 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j^0 } is the nonresonant refractive index in the IR wavenumber region. In the reference paper [2], we use the refractive index values in the visible regions to fit Cauchy's equation.
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j^0(\lambda) = A + \frac{B}{{\lambda}^2} + \frac{C}{{\lambda}^4}}
The obtained parameters 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A, B, C} were used to evaluate the nonresnant refractive index at 5000 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \text{cm}^{-1} } .
It is also possible to directly use the refractive index in the visible region, which may involve a very slight deviation in 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j^0 } . [2]
After the determination of 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j^0 } , other parameters related to the Lorentz functions are determined by minimizing the least-squares residual (LSR) between the experimental reflectance spectra and those of the analytical formulas over the whole wavenumber region of the target vibrational band. The residual is defined by
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \text{LSR} ( \{ A_l, \nu_l, \Gamma_l \} ) = \frac{1}{n} \sum_{\nu_n \in [\nu_\text{min}, \nu_\text{max}]} \left[ |r_{ij}^p (\nu_n)|^2 + |r_{ij}^s (\nu_n)|^2 - 2|r_{ij} (\nu_n)|^2_\mathrm{exp} \right]^2 }
where 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle | r_{ij}^p|^2 } and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle | r_{ij}^s|^2 } are the calculated reflectances in the above section. 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle |r_{ij} (\nu_n)|^2_\mathrm{exp} } is the experimental reflectance of unpolarized light at wavenumber 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \nu_n } . The summation of 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n } is taken for all observed wavenumber points in the target vibrational band. By minimizing the LSR, the parameters of each Lorentz functions, 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_l } , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \nu_l} and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \Gamma_l} , were obtained. The minimization is numerically done in the program, thus the initial parameter of 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle l_\text{max} } , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_l } , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \nu_l} and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \Gamma_l} should be determined. And the initial parameters also have a large effect on whether the minimization can reach the tolerance and how long the minimization procedure is taken. All of them can be set manually. In the following, we will introduce a method to automatically determine the initial parameters.
In order to determine the number of Lorentz functions to be used, we first start with only one Lorentz function and represent the complex refractive index as
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j (\nu) = n_j^0 + \frac{A_1}{\nu_1 - \nu - i \Gamma_1} }
The first Lorentz function is used to fit the strongest adsorption band in the target region. Thus, the initial parameter for 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \nu_1 } is set to the wavenumber of minimum value of reflectance in the experimental data. The initial parameter for 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \Gamma_1 } and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_1 } are set according to the lineshape of strongest adsorption band in ATR-IR spectra.
After the first fitting procedure, the strongest adsorption band is expected to be well represented. Here if the LSR is less than the tolerance, the fitting is finished and no more Lorentz functions are required. If not, another Lorentz function is added and the complex refractive index become
- 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle n_j (\nu) = n_j^0 + \frac{A_1}{\nu_1 - \nu - i \Gamma_1} + \frac{A_2}{\nu_2 - \nu - i \Gamma_2} }
The second Lorentz funtion is used to represent major adsorption band in the difference reflectance spectra between the first fitting results and experimental results. The initial value of 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \nu_1 } , 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \Gamma_1 } and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_1 } are set to be the optimized value in the last fitting procedure. The initial value of 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \nu_2 } is set to the wavenumber of minimum (or maximum) value of difference reflectance spectra. The initial parameter for 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \Gamma_2 } and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_2 } is set to be 15 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle \text{cm}^{-1} } and 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle 0.5 A_1 \text{cm}^{-1} } , respectively. A smaller initial value of 構文解析に失敗 (MathML、ただし動作しない場合はSVGかPNGで代替（最新ブラウザーや補助ツールに推奨）: サーバー「https://wikimedia.org/api/rest_v1/」から無効な応答 ("Math extension cannot connect to Restbase."):): {\displaystyle A_2 } suggests that the second Lorentz function is a minor adsorption band in ATR-IR spectra. Then all parameters are again optimized using the same fitting procedure.
The number of Lorentz functions keeps increasing and the whole procedure is repeated until the final LSR reaches the set tolerance.
- ↑ "Theory of Sum Frequency Generation Spectroscopy" Akihiro Morita. Springer Nature Singapore Pte Ltd: 2018
- ↑ 2.0 2.1 "Dispersion of Complex Refractive Indices for Intense Vibrational Bands. I Quantitative Spectra" Ryo Murata, Ken-ichi Inoue, Lin Wang, Shen Ye, and Akihiro Morita, J. Phys. Chem. B, 125(34), 9794-9803 (2021).